Lär Dig Använda Sannolikhet I Poker För Att Öka Dina Vinster

Poker är ett spel som är i stort sett baserat på matte och statistik. En vinst inte alltid är garanterad, men att spela en strategi som bidrar till att följa korrekta pokersannolikheter och odds kommer utan tvekan att öka dina chanser att lyckas.

I denna artikel bryter vi ner pokeroddsen och de sannolikheter som är associerade med spelet för att hjälpa dig att förstå sannolikheten för specifika spel och också för att lära dig hur man spelar poker med sannolikhet i åtanke.

Innehållsförteckning

•    Sannolikhet för Pokerhänder 
•    Hur Man Kommer Fram Till Sannolikheten För En Pokerhand
•    Oddsen För att Få Ett Specifikt Handkort i Poker? 
•    Odds För Att Vända En Given Hand
•    Vad händer om jag själv vill öva sannolikheten för poker?

Det finns 2 598 960 distinkta 5-kortshänder som kan fås / delas ut i poker. I nedan pokersannolikhetschema tar vi oss en närmare titt på hur dessa kombinationer bryts ner i olika rader av händer som man kan uppnå:

Det finns några viktiga saker att notera från denna tabell: 

•    Rankningen av händer går upp sekventiellt från den enklaste handen till den svåraste (otroligaste) att få. (Därför vet du nu exakt varför flush rankas högre än straight i Texas Hold'em.)
•    Sannolikheten för ett par i poker är ~ 42%.
•    Sannolikheten att du får en kåk är mindre än 1% (~ 0,1441%)
•    Sannolikheten för att få royal flush i poker Texas Hold'em är bara 1 av 649 740 händer!
•    Sannolikheten för en straight flush i poker är 1 av 72 193 händer eller 0,00139%.

Du kan referera till detta diagram när du bestämmer hur sannolikt det är att en specifik pokerhand visas i ett spel.

Hur Man Kommer Fram Till Sannolikheten För En Pokerhand

Vad är sannolikheten för att få två par i poker?
Vad är möjligheten att få en straight i poker?
Vad är sannolikheten för en kåk i poker?

I vår 888poker Magazine har vi en mängd artiklar som redan innehåller alla svar på dina brinnande frågor om sannolikheter och odds angående specifika pokerhänder.

Oddsen För att Få Ett Specifikt Handkort i Poker? 

Multiplicera 52 kort i en standardlek med 51 (för det andra kortet) och dela sedan produkten med 2 (eftersom AcKs är samma sak som att få KsAc - bara att ordning som den delas in är omvänd). Du ser att det finns 1 326 unika 2-kortkombinationer du kan få i Texas Hold'em.

 
Vi kan bryta ner detta ytterligare, om du tar en hand med AK, kan du multiplicera de 4 essen med 4 kungar för att se att det finns 16 kombinationer av AK totalt, både i samma färg och olika.

Av dessa 16 kombinationer, eftersom det finns fyra olika färger i poker, kommer 4 av dessa AK-kombinationer att passa, vilket gör att det finns 12 ofärgade kombinationer av oparade händer. (Samma siffror gäller alla icke-parade pokerhänder). För hand-par kommer det att finnas sex kombinationer av varje värde.

Genom att känna till ovanstående information kan vi sedan använda oss av grundläggande matematik för att avgöra sannolikheten för att få vissa kombinationer av handkort.

Till exempel, för hand ecc, delar vi 6 kombinationer med 1 326 totala kombinationer för att se att vi i genomsnitt får denna hand 1 gång av 221 händer.

För varje specifik färgad hand, eftersom det bara finns fyra kombinationer av varje innehav (istället för 6 som med hand-paren), får du händer med färgade icke-par (med specifika värden) mer sällan än vad du kommer att få hand-par. Därför får du en hand som AKs, 1 gång på 332 händer, i genomsnitt, vilket innebär att du får AA oftare än du kommer att få AK.

Till den sista punkten i detta avsnitt, om du vill ta reda på chanserna att få hand X eller bättre, lägg bara till antalet kombinationer för varje innehav.

Till exempel, om vi vill hitta chanserna att få QQ + och / eller AK, ser vi att det finns 18 kombinationer av hand-par och 16 kombinationer av AK, vilket ger totalt 34 kombinationer.

Om vi delar 1 326 kombinationer totalt med 34 av dessa specifika kombinationer betyder det att du får AK eller QQ + ungefär 1 av 39 händer.

Här är ett diagram som sammanfattar informationen som vi precis gått igenom om hand-korten, dessutom innehåller den även andra sannolikheter för att få särskilda kombinationer på vissa innehav:

Ovanstående avsnitt handlade om sannolikheten för att få vissa kombinationer av hand-kort. Men vad säger pokeroddsen om hur dessa hand-kort kommer att förbättras (och i vilken grad) på specifika floppar?

Här är ett diagram över olika sannolikheter för hand-kort som du kan kolla igenom och lära dig när det gäller chanserna att vända en given hand (av varierande styrkor):

Poker Oddsen: Förbättra Din Draghand

En "out" i poker är ett kort som kommer hjälpa dig att förbättra styrkan i din hand. De vanligaste out-korten är de som hjälper en spelare att få flush eller straight.
Här är en tabell som förklarar oddsen för att förbättra din hand, beroende på antalet outs du har:

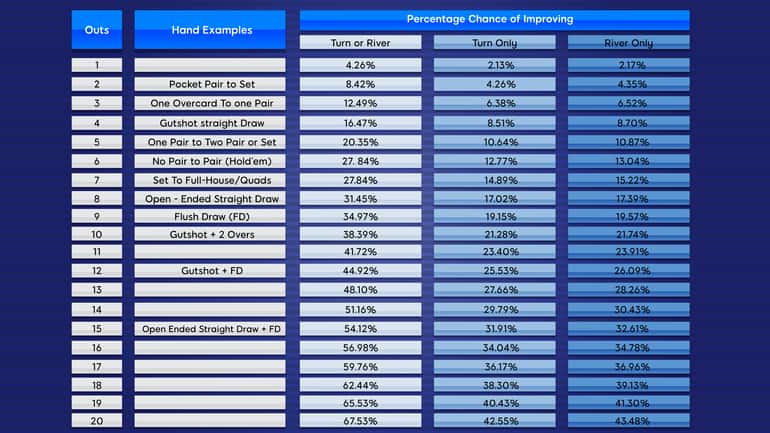
 Grundläggande Sannolikhetsregler För Poker

Det kommer naturligtvis att vara svårt att hänvisa till det här diagrammet för varje hand för att se vilka chanser du har för att förbättra dig och sedan relatera detta till de potentiella oddsen du får. Så, för att ge dig en grundläggande genväg, använd följande trick för att veta hur du beräknar sannolikheten för att dina pokerhänder förbättras:

Om du multiplicerar antalet outs du har på floppen med 4 får du en bra uppskattning för chansen att få din hand vid vändning eller river (dvs med två kort som kommer).

Om du multiplicerar antalet outs som du har på floppen eller vändningen med 2 får du en tillförlitlig uppskattning för chansen att få din hand på nästa kort.

Ibland vill du kanske variera antalet outs som hjälper dig att förbättra din hand, för att ta hänsyn till chanserna att det också hjälper din motståndare att förbättra till en ännu bättre hand.

Till exempel, om du tror att din motståndare kan ha en högre speldragning eller om bord paret ger dig en flush och din motståndare kanske har kåk, kan du minska dina "outs" något (t.ex. 8,5 outs istället för 9). Denna justering kommer att ta hänsyn till möjligheten när den kopplas till dina pott-odds och hur du ska gå vidare med handen.

Metoden bakom att öva på pokersannolikhetsproblem utan att använda stenografi kan fortfarande göras.

För att göra detta måste du lägga till sannolikheten för att ett specifikt resultat uppstår, till exempel:

•    Att få en av dina outs på vändningen
•    Att få en av dina outs på rivern, men inte vändningen

EXEMPEL PROBLEM #1: En Normal Flushdragning

För att arbeta dig igenom ett typiskt sannolikhetsproblem, antar att du har ett flushdrag efter floppen och bara vill veta chanserna att förbättra till en flush vid rivern.
Med 4 av 13 kort i samma färg redan synliga finns det 9 återstående kort ("outs") som kan hjälpa dig.

Och med två hålkort och tre floppkort som redan redovisas finns det 47 okända kort kvar i kortlekarna.

Genom att veta detta kan du göra lämpliga beräkningar och lägga ihop resultaten för att bestämma dina chanser att få din flush:

•    Oddsen för att slå din flush vid vändningen: (9/47) = 19,15%
•    Oddsen för att slå din flush vid rivern: (39/47) * (9/46) = 16,23%
•    Oddsen för att få en flush vid vändning ELLER rivern: 19,15% + 16,23% = 35,38%

Här kan du se att oddsen för att få en flush vid rivern efter att ha vänt en flushdragning är 35,38%. Om du tar "genvägs" -regeln som beskrivs ovan kan du se att 9 outs multiplicerat med 4 är lika med 36%, vilket är ganska nära det exakta svaret här.

EXEMPEL PROBLEM #2: En Bakdörrs-Flushdragning 

För att öva på sannolikheten att träffa en bakdörrs-flush måste du multiplicera (10 flush outs / 47 okända kort) för turen med (9 flush outs / 46 okända kort) på rivern. Resultatet skulle visa att det finns en ~ 4,2% chans att en 3-flush på floppen blir en full, 5-kortsflush vid rivern.

Beräkna Sannolikheten För En Pokerhands Head-Up

En viktig sak att notera i poker är skillnaden i kapitalutdelning när det bara finns en motståndare jämfört med när det finns flera motståndare till dig på en pokerhand.
Mot många spelare kommer kapitalet i allas respektive händer att bli lägre än om det vore head-up eftersom det kommer att delas upp och spridas bland de andra återstående spelarna.

Ta till exempel Pocket Aces. Mot följande skurksteg för din motståndare (n) -

•    Alla hand-par
•    Alla färgade ess
•    Två broadway-kort 
•    Färgade kontakter: 54 till T9
•    Ett-gaps färgade kontakter: 86s till J9s
•    Q9s, K9s

Här är de andelar som Pocket ess har emot:

•    En motståndare: 83,4%
•    Två motståndare: 70,6%
•    Tre motståndare: 60,2%
•    Fyra motståndare: 51,4%

Som du kan se, desto fler motståndare det finns i en hand, desto lägre är chansen att AA vinner. Det är därför det är så fördelaktigt att ha dessa stora par utspelade i en heads-up, låg-SPR-pott.

Och när det är din tur att dra i ett flervägsscenario kan det hända att fler motståndare inte ändrar antalet outs du måste förbättra. Men chanserna för att någon annan ska få ett bättre drag än dig eller en hand som senare kan slå din ökar med fler motståndare. 

Dessutom är det viktigt att notera att spelare tenderar att bluffa mindre och satsa mer för värde om de satsar när det är flera vägar.

Därför, med tanke på de två sista poängen, är det viktigt att alltid komma ihåg hur många motståndare som finns för en hand och därefter bestämma det bästa sättet att spela på.

Sammanfattning av pokersannolikhet

För att öka sannolikheten för att vinna poker måste du vänja dig vid de odds och sannolikheter som presenteras för dig i spelet. Bli bekant med outs och beräkna dina procentsatser för att förbättra dig och kunna snabbt relatera dessa till de potentiella odds du kan få, så att du kan avgöra om du kan syna lönsamt eller inte.

Kom också ihåg att du inte alltid behöver ”bara syna” när du drar. Ibland kan det vara fördelaktigt att satsa eller höja. På så sätt kan du antingen vinna genom att senare förbättra den bästa handen eller få din motståndare att lägga sig.

Sammanfattningsvis och för att citera The Hunger Games: "Må (poker) oddsen alltid vara till din fördel!" Lycka till med spelen!